代码随想录-数组

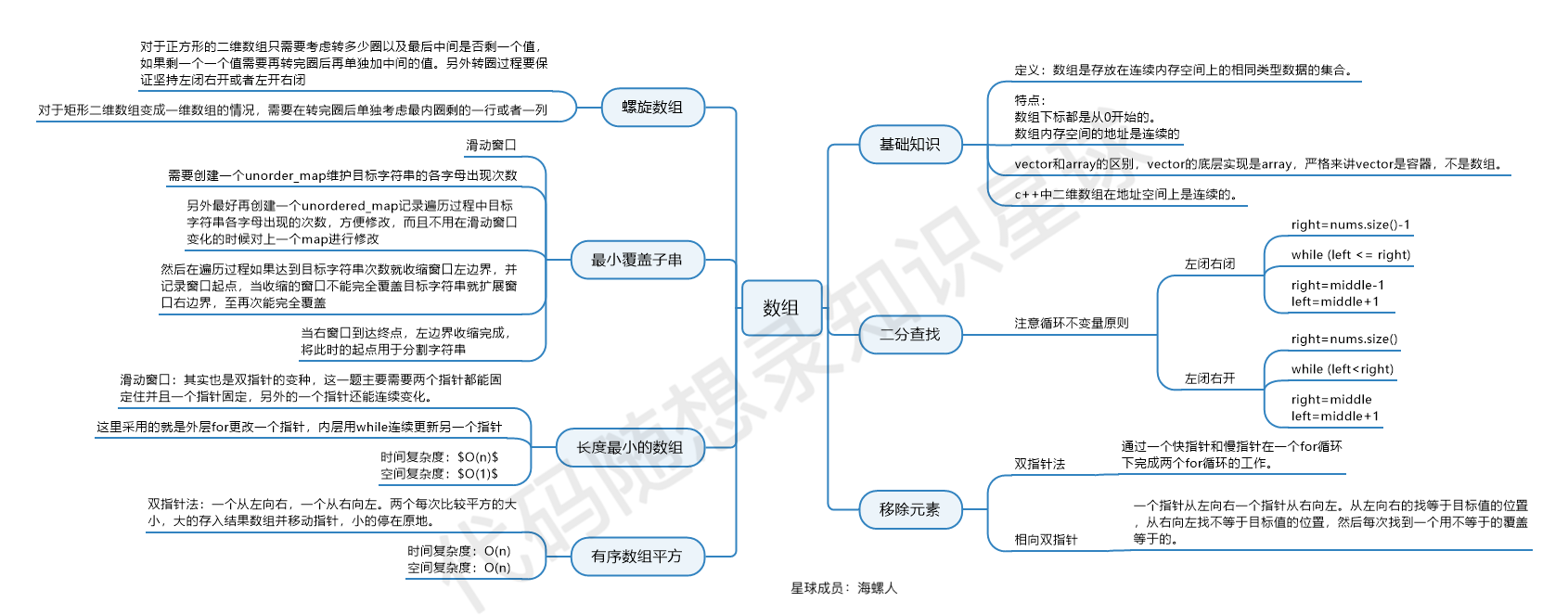
数组理论基础

数组是存放在连续内存空间上的相同类型数据的集合。

数组下标都是从0开始的。
数组内存空间的地址是连续的

为什么删除元素需要移动？

假设我们有一个数组 [a, b, c, d]，存储在地址 1000、1004、1008、1012。现在我们要删除第 2 个元素 b（地址 1004）。删除后，如果什么都不做，内存里会变成 [a, (空), c, d]，地址是 1000、1004（空）、1008、1012。这样就出现了一个空隙，地址不再连续，数组的结构就被破坏了。

为了保持数组的连续性，我们需要：

将 c 从地址 1008 移动到 1004（填补 b 删除后的空位）。
将 d 从地址 1012 移动到 1008。
最终数组变成 [a, c, d]，地址是 1000、1004、1008，仍然是连续的。

原因总结：如果不移动元素，删除后会留下空隙，导致数组不再连续。而数组的定义要求元素必须连续存储，所以必须通过移动后续元素来填补空隙。

为什么增添元素需要移动？

现在假设我们想在第 2 个位置插入一个新元素 e，原来的数组是 [a, c, d]，地址是 1000、1004、1008。我们希望结果变成 [a, e, c, d]。

但问题在于，地址 1004 已经被 c 占用，后面也都是连续的，没有空隙直接放入 e。为了给 e 腾出空间，我们需要：

先将 d 从 1008 移动到 1012。
然后将 c 从 1004 移动到 1008。
最后将 e 放入 1004。
结果是 [a, e, c, d]，地址变成 1000、1004、1008、1012，仍然是连续的。

原因总结：因为数组是连续的，没有多余的空间直接插入新元素，必须通过移动已有元素来腾出位置，同时保持所有元素地址的连续性。

1. vector 和 array 的区别

**vector**：
- 是 C++ 标准模板库（STL）中的一种容器。
- 它是一个动态数组的封装，意思是它的大小可以根据需要自动调整。
- 当你添加或删除元素时，vector 会自动管理内存，比如在容量不足时重新分配更大的内存块。
- 使用场景：需要动态调整大小的序列数据。
**array**（这里指的是 std::array）：
- 是 C++11 引入的一种固定大小数组的封装。
- 大小在编译时就必须确定，运行时无法改变。
- 它是对传统 C 风格数组（如 int arr[10]）的改进，提供了更好的接口，但依然是固定长度的。
- 使用场景：需要固定大小且已知元素数量的数据。

两者的核心区别在于：**vector 是动态的，而 std::array 是静态的**。

2. “严格来讲 vector 是容器，不是数组”

容器：
- 在 C++ 中，“容器”是一个更广义的概念，指的是 STL 中用于存储和管理元素的数据结构，比如 vector、list、map 等。
- vector 作为一个容器，不仅提供了数据存储，还封装了许多操作（如 push_back、resize 等）和自动内存管理。
数组：
- 通常指的是一块连续的内存，用于存储相同类型的元素，比如 C 风格数组（int arr[10]）或 std::array。
- 数组本身没有动态调整大小的能力，也没有像容器那样的丰富接口。
区别：
- vector 虽然表现得像一个数组（连续内存、可通过索引访问），但它本质上是一个容器，提供了比普通数组更多的功能和灵活性。

二分查找

写二分法，区间的定义一般为两种，左闭右闭即[left, right]，或者左闭右开即[left, right)。
区间的定义就是不变量
前提是数组为有序数组，数组中无重复元素

时间复杂度：O(log n)
- 最坏情况：
  - 最坏情况发生在目标值不在数组中，或者位于区间的边界。此时，循环会一直执行，直到 left > right 时退出。
  - 每次循环将区间大小从当前值（假设为 k）缩小到大约 k/2：
    - 初始区间大小：n。
    - 第 1 次循环后：n/2。
    - 第 2 次循环后：n/4。
    - 第 3 次循环后：n/8。
    - …
    - 第 k 次循环后：n / 2^k。
  - 循环终止条件是区间大小小于 1，即 n / 2^k < 1，也就是 2^k > n。
  - 因此，循环次数 k 满足 k ≈ log₂(n)（对数以 2 为底），实际中需要向上取整，但渐进分析中忽略常数。
- 时间复杂度结论：
  - 每次循环的计算（中点计算和比较）是 O(1)。
  - 循环执行 O(log n) 次。
  - 总时间复杂度 = O(1) × O(log n) = **O(log n)**。
空间复杂度：O(1)
- 空间使用特点
  - 这些变量都是基本数据类型（int），每个占用固定大小的内存（通常是 4 或 8 字节，取决于系统架构）。
  - 变量数量固定为 3 个，与输入数组的大小 n 无关。
  - 没有递归调用（如果是递归实现，可能会有栈空间开销，但这里是迭代实现）。

class Solution {
public:
    int search(vector<int>& nums, int target) {
        int left = 0;
        int right = nums.size() - 1;
        while (left <= right) {
            int middle = left + ((right - left) / 2);
            if (nums[middle] > target) {
                right = middle - 1;
            } else if (nums[middle] < target) {
                left = middle + 1;
            } else {
                return middle;
            }
        }
        return -1;
    }
};

语法关键点总结

类型声明：C++ 需要显式声明变量和函数的类型（如 int、vector<int>），Python 不需要。
代码块：C++ 用 {} 定义代码块，Python 用缩进。
动态数组：vector<int> 类似 Python 的 list，nums.size() 类似 len(nums)。
**引用 &**：表示传递数据的引用，类似 Python 中列表的默认行为。
访问控制：public: 是 C++ 特有，Python 没有。
整除：C++ 的 / 对整数自动向下取整，Python 用 //。
((right - left) >> 1) 中的 >> 是 C++ 中的右移运算符。右移 1 位相当于将一个数除以 2 并向下取整（对于正数而言）。
因此，((right - left) >> 1) 等价于 (right - left) / 2，表示区间长度的一半。

class Solution:
    def search(self, nums: List[int], target: int) -> int:
        left, right = 0, len(nums)  # 定义target在左闭右开的区间里，即：[left, right)

        while left < right:  # 因为left == right的时候，在[left, right)是无效的空间，所以使用 <
            middle = left + (right - left) // 2

            if nums[middle] > target:
                right = middle  # target 在左区间，在[left, middle)中
            elif nums[middle] < target:
                left = middle + 1  # target 在右区间，在[middle + 1, right)中
            else:
                return middle  # 数组中找到目标值，直接返回下标
        return -1  # 未找到目标值

语法关键点总结.

def search(self, nums: List[int], target: int) -> int:**

语法含义：
- def：定义函数的关键字。
- search：函数名。
- self：类的实例参数，必须显式写出，表示调用该方法的对象本身。
- nums: List[int]：参数 nums 的类型提示，List[int] 表示 nums 是一个包含整数的列表（来自 typing 模块）。
- target: int：参数 target 的类型提示，表示它是一个整数。
- -> int：返回类型提示，表示函数返回一个整数。
特点：类型提示（如 List[int] 和 -> int）是 Python 3.5+ 的特性，用于提高代码可读性，但不强制执行。
作用：定义了一个实例方法 search，接受列表 nums 和整数 target，并返回一个整数。

移除元素

“超出新长度后面的元素”是什么意思？

这个说法指的是：数组在移除指定元素后，会有一个新的“有效长度”（即剩下的元素个数）。而数组的实际长度（内存中分配的空间）可能比这个有效长度大。题目告诉你，不需要关心或处理那些超出有效长度后面的部分。
简单来说：

你只需要保证数组的前 k 个元素（k 是新长度）是移除 val 后的结果。
数组后面剩下的部分（从第 k 个位置到末尾）可能还有一些原来的元素，但这些元素不会被认为是结果的一部分，所以不用管它们。

双指针法（快慢指针法）： 通过一个快指针和慢指针在一个for循环下完成两个for循环的工作。

快指针：寻找新数组的元素，新数组就是不含有目标元素的数组

慢指针：指向更新新数组下标的位置

class Solution {
public:
    int removeElement(vector<int>& nums, int val) {
        int slowIndex = 0;
        for (int fastIndex = 0; fastIndex < nums.size(); fastIndex++) {
            if (val != nums[fastIndex]) {
                nums[slowIndex++] = nums[fastIndex];
            }
        }
        return slowIndex;
    }
};

执行顺序总结

for 循环初始化：fastIndex = 0。
条件检查：fastIndex < nums.size()，决定是否进入循环。
循环体：
- 判断：if (val != nums[fastIndex])，检查当前元素是否需要保留。
- 赋值和自增：如果条件为真，执行 nums[slowIndex++] = nums[fastIndex]：
  - 先用当前 slowIndex 的值作为下标，把 nums[fastIndex] 赋值过去。
  - 然后 slowIndex 自增 1。
fastIndex 自增：每次循环结束，fastIndex++。
重复 2-4，直到 fastIndex < nums.size() 为假。

时间复杂度：O(n)

空间复杂度：O(1)

（版本二）暴力法
class Solution:
    def removeElement(self, nums: List[int], val: int) -> int:
        i, l = 0, len(nums)
        while i < l:
            if nums[i] == val: # 找到等于目标值的节点
                for j in range(i+1, l): # 移除该元素，并将后面元素向前平移
                    nums[j - 1] = nums[j]
                l -= 1
                i -= 1
            i += 1
        return l

i -= 1 的作用是让指针 i 回退一步，以便在移除元素并调整数组后重新检查当前位置。这是必要的，因为平移操作可能会引入一个新的需要检查的元素到 nums[i] 的位置。

class Solution:
    def removeElement(self, nums: List[int], val: int) -> int:
        n = len(nums)
        left, right  = 0, n - 1
        while left <= right:
            while left <= right and nums[left] != val:
                left += 1
            while left <= right and nums[right] == val:
                right -= 1
            if left < right:
                nums[left] = nums[right]
                left += 1
                right -= 1
        return left

`result(A.size(), 0)`**

这是 vector 类的一个构造函数调用。
语法：vector<T>(size_t n, const T& val)。
- 第一个参数 n：指定向量的大小（元素个数）。
- 第二个参数 val：指定初始化的值，所有元素都被初始化为这个值。
具体含义：
- A.size()：返回输入向量 A 的元素个数（假设为 n）。
- 0：每个元素初始化为 0。
  平方的大小比较直接相加与0进行比较即可
  逆序遍历：
range(len(nums)-1, -1, -1) 是 Python 中逆序遍历列表索引的标准方式。
从最后一个元素到第一个元素，适合需要从尾部开始处理的场景。
range 的 stop 是独占的（不包含），所以 -1 表示停止在 0 之前。

长度最小的子数组

lass Solution:
    def minSubArrayLen(self, s: int, nums: List[int]) -> int:
        l = len(nums)
        left = 0
        right = 0
        min_len = float('inf')
        cur_sum = 0 #当前的累加值
        
        while right < l:
            cur_sum += nums[right]
            
            while cur_sum >= s: # 当前累加值大于目标值
                min_len = min(min_len, right - left + 1)
                cur_sum -= nums[left]
                left += 1
            
            right += 1
        
        return min_len if min_len != float('inf') else 0

C++ 中有 INT_MAX 吗？ 有，来自。
区别：INT_MAX 依赖 int 大小，INT32_MAX 固定为 32 位最大值。
建议：现代 C++ 中，推荐用的固定宽度常量（如 INT32_MAX），以提高代码的可移植性和清晰度。
C 中的 INT_MAX 来自什么库？
- 来自 <limits.h>，表示 int 类型的最大值。
C 中有 INT32_MAX 吗？
- 在 C99 及之后有，来自 <stdint.h>，表示 32 位有符号整数的最大值。
- 在 C89 中没有。
  在 C 中使用建议：
如果只需要基本的 int 限制，用 <limits.h> 的 INT_MAX。
如果需要固定 32 位整数，用 <stdint.h> 的 INT32_MAX（确保编译器支持 C99）。

螺旋矩阵

vector<vector<int>> 是一个二维动态数组。
坚持一致的左闭右开，或者左开右闭的原则，这样这一圈才能按照统一的规则画下来。

两种写法的对比

**1. `nums = [[0] * n for _ in range(n)]`**

含义：
- 使用列表推导式，循环 n 次，每次创建一个独立的 [0] * n 列表。
- 结果是一个 n x n 的二维列表，每个内层列表是独立的。
内存结构：
- 外层列表包含 n 个不同的内层列表对象。

示例（n = 3）：

1 2	`nums = [[0] * 3 for _ in range(3)] # nums = [[0, 0, 0], [0, 0, 0], [0, 0, 0]]`

行为：

修改某一行不会影响其他行。

1 2	`nums[0][0] = 1 print(nums) # [[1, 0, 0], [0, 0, 0], [0, 0, 0]]`

**2. `nums = [[0] * n] * n`**

含义：
- 先创建单个 [0] * n 列表（长度为 n 的全零列表）。
- 然后用 * n 将这个列表重复 n 次，形成一个二维列表。
内存结构：
- 外层列表包含 n 个元素，但它们全都引用同一个内层列表对象（浅拷贝）。

示例（n = 3）：

1 2	`nums = [[0] * 3] * 3 # nums = [[0, 0, 0], [0, 0, 0], [0, 0, 0]]（表面上看一样）`

行为：

修改某一行会影响所有行，因为它们是同一个对象。

1 2	`nums[0][0] = 1 print(nums) # [[1, 0, 0], [1, 0, 0], [1, 0, 0]]（所有行都变）`

关键区别：引用问题

引用 vs 独立对象

**[[0] * n for _ in range(n)]**：
- 每次循环调用 [0] * n，创建新的独立列表。
- 外层列表的每个元素是不同的对象，内存地址不同。
- 检查内存地址：
  1
  2
  nums = [[0] * 3 for _ in range(3)] print([id(row) for row in nums]) # [不同地址1, 不同地址2, 不同地址3]
**[[0] * n] * n**：
- 只创建一次 [0] * n，然后通过 * 重复引用这个对象。
- 外层列表的每个元素指向同一个内层列表，内存地址相同。
- 检查内存地址：
  1
  2
  nums = [[0] * 3] * 3 print([id(row) for row in nums]) # [同一地址, 同一地址, 同一地址]

浅拷贝效应

在 Python 中，* 操作对列表是浅拷贝：

它复制引用，而不是创建新对象。
对于不可变对象（如整数 0），* 没有问题。

对于可变对象（如列表 [0]），会导致所有引用指向同一个对象。

int** generateMatrix(int n, int* returnSize, int** returnColumnSizes){
    //初始化返回的结果数组的大小
    *returnSize = n;
    *returnColumnSizes = (int*)malloc(sizeof(int) * n);
    //初始化返回结果数组ans
    int** ans = (int**)malloc(sizeof(int*) * n);
    int i;
    for(i = 0; i < n; i++) {
        ans[i] = (int*)malloc(sizeof(int) * n);
        (*returnColumnSizes)[i] = n;
    }

语法：
- **for(i = 0; i < n; i++)**：
  - i = 0：初始化循环变量 i 为 0。
  - i < n：条件，当 i < n 时执行循环体。
  - i++：每次迭代后 i 增加 1。
  - 循环范围：i = 0, 1, …, n-1。
- *ans[i] = (int)malloc(sizeof(int) * n);**：
  - ans[i]：访问 ans 的第 i 个元素（一个 int*）。
  - (int*)：将 malloc 的 void* 转换为 int*。
  - malloc(sizeof(int) * n)：为一行分配 n 个整数的内存。
  - =：将分配的内存地址赋给 ans[i]。
- **(*returnColumnSizes)[i] = n;**：
  - *returnColumnSizes：解引用得到列大小数组的指针。
  - (*returnColumnSizes)[i]：访问第 i 个元素。
  - = n：将 n 赋给该元素，表示第 i 行的列数是 n。
意义：
- 循环 n 次，为矩阵的每一行分配内存，并设置列大小。
- 示例（n = 3）：
  - ans[0] = malloc(12)：第 0 行，分配 3 个整数。
  - ans[1] = malloc(12)：第 1 行。
  - ans[2] = malloc(12)：第 2 行。
  - (*returnColumnSizes)[0] = 3, [1] = 3, [2] = 3：每行有 3 列。
解引用顺序：
(*returnColumnSizes)[i]：先解引用再索引，等价于 returnColumnSizes[0][i]。

区间和

前缀和的思想是重复利用计算过的子数组之和，从而降低区间查询需要累加计算的次数。
前缀和在涉及计算区间和的问题时非常有用！

#include <iostream>
#include <vector>
using namespace std;
int main() {
    int n, a, b;
    cin >> n;
    vector<int> vec(n);
    vector<int> p(n);
    int presum = 0;
    for (int i = 0; i < n; i++) {
        scanf("%d", &vec[i]);
        presum += vec[i];
        p[i] = presum;
    }

    while (~scanf("%d%d", &a, &b)) {
        int sum;
        if (a == 0) sum = p[b];
        else sum = p[b] - p[a - 1];
        printf("%d\n", sum);
    }
}

在 C++ 中，使用 std::cin 和 std::cout 时，默认会与 C 语言的标准 I/O（stdio）进行同步，以保证混用时的数据正确性。但这种同步机制会带来额外的开销，尤其在处理大量数据时，这部分开销就显得尤为明显。相比之下，scanf 和 printf 直接调用 C 标准库的函数，不存在这种同步过程，因此在大量数据的读写操作中，它们通常会快得多。
在 scanf 函数中，"%d" 是一个格式控制符，表示期望输入的是一个十进制整数。
在二进制补码表示法中，-1 的二进制形式是所有位都是 1。取反（~ 操作符）会把每一位都变成相反的值，所以 ~(-1) 就会变成所有位为 0，也就是整数 0。
对于 scanf，当成功读取数据时，它返回读取成功的项数（例如，读取两个整数则返回 2），这些数值在二进制补码中并不全是 1，取反后肯定不会得到 0。因此，只有当 scanf 遇到文件结束（EOF）返回 -1 时，~(-1) 才会等于 0，从而结束循环。

import sys
input = sys.stdin.read

def main():
    data = input().split()
    index = 0
    n = int(data[index])
    index += 1
    vec = []
    for i in range(n):
        vec.append(int(data[index + i]))
    index += n

    p = [0] * n
    presum = 0
    for i in range(n):
        presum += vec[i]
        p[i] = presum

    results = []
    while index < len(data):
        a = int(data[index])
        b = int(data[index + 1])
        index += 2

        if a == 0:
            sum_value = p[b]
        else:
            sum_value = p[b] - p[a - 1]

        results.append(sum_value)

    for result in results:
        print(result)

if __name__ == "__main__":
    main()

在 Python 中，sys.stdin.read 是一个方法，用于一次性读取标准输入（通常是从键盘输入或重定向的文件）的所有内容。将它赋值给 input 意味着你用 input() 调用时，就会执行 sys.stdin.read() 方法，返回整个输入字符串。
查询输入：
while index < len(data): 表示只要还有未处理的数据，就继续循环。每次循环从 data 中取出两个数字，分别赋值给 a 和 b，这两个数字代表一个查询区间的起始和结束下标。

#include <stdio.h>
#include <stdlib.h>

int main(int argc, char *argv[])
{
    int num;
    // 读取数组长度
    scanf("%d", &num);

    // 使用动态内存分配而不是静态数组，以适应不同的输入大小
    int *a = (int *)malloc((num + 1) * sizeof(int));

    // 初始化前缀和数组的第一个元素为0
    a[0] = 0;

    // 读取数组元素并计算前缀和
    for (int i = 1; i <= num; i++)
    {
        int mm;
        scanf("%d", &mm);
        // 累加前缀和
        a[i] = a[i - 1] + mm;
    }

    int m, n;
    // 循环读取区间并计算区间和，直到输入结束
    // scanf()返回成功匹配和赋值的个数,到达文件末尾则返回 EOF
    while (scanf("%d%d", &m, &n) == 2)
    {
        // 输出区间和，注意区间是左闭右开，因此a[n+1]是包含n的元素的前缀和
        printf("%d\n", a[n+1] - a[m]);
    }

    // 释放之前分配的内存
    free(a);
    return 0;
}

scanf 返回值：
scanf 函数在读取输入时，会返回成功读入的变量个数。
在这个代码中：

a[i] = 从0到i-1的元素和，所以：
- a[n+1] = 从0到n的元素和，
- a[m] = 从0到m-1的元素和。
  a[n+1] - a[m] = (从0到n的和) - (从0到m-1的和) = 从m到n的元素和

leetcode master

代码随想录-数组

https://blakehansen130.github.io/2025/03/06/代码随想录-数组/

发布于

2025年3月6日

许可协议

黑马python第二阶段第一章下一篇

代码随想录-数组

代码随想录-数组

数组理论基础

为什么删除元素需要移动？

为什么增添元素需要移动？

1. vector 和 array 的区别

2. “严格来讲 vector 是容器，不是数组”

二分查找

语法关键点总结

语法关键点总结.

移除元素

“超出新长度后面的元素”是什么意思？

执行顺序总结

result(A.size(), 0)**

长度最小的子数组

螺旋矩阵

两种写法的对比

1. nums = [[0] * n for _ in range(n)]

2. nums = [[0] * n] * n

关键区别：引用问题

引用 vs 独立对象

浅拷贝效应

区间和

`result(A.size(), 0)`**

**1. `nums = [[0] * n for _ in range(n)]`**

**2. `nums = [[0] * n] * n`**